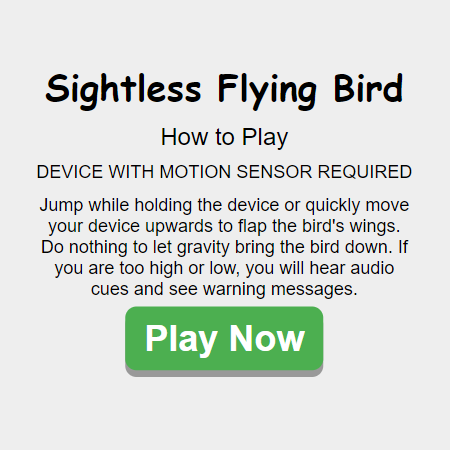
Our Apps & Products

Rows & Tables - The SQL Card Game
We live in an age where DATA is the new GOLD, compete against others in a game that introduces kids & adults to REAL DATA SCIENCE!
Click the Link Below to Learn More

This is Bull
Can you keep catching the bull for more than 15 seconds? Push your tapping, agility, and quick thinking to the limits.
Click the Links Below to Access the App

Saiyan Tap Trainer
As a huge fan of the Dragon Ball series by Akira Toriyama, this clicker game serves as a fan art tribute to the show.
Click the Links Below to Access the App
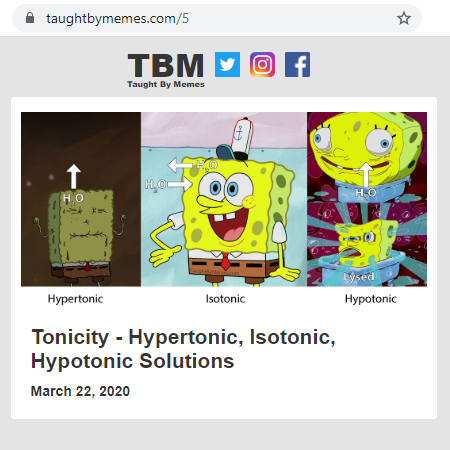
TaughtByMemes.com
Making education relevant to today's generation, get taught by memes!
Click the Links Below to Access the App
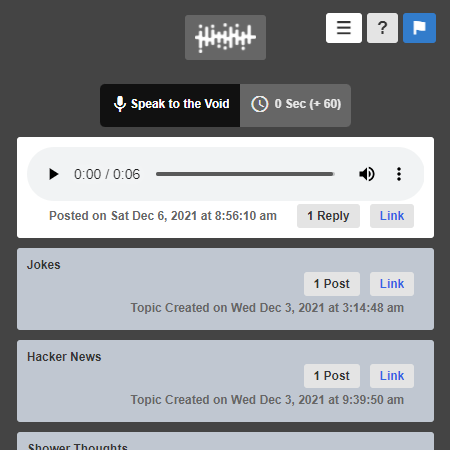
VocalVoid.com
Audio based, open forum. Anyone can record and post an audio clip up to a minute about anything.
Click the Links Below to Try It

hizzah.com
The best place for people attain short term loans through crowdsourcing. An alternative to asking for donations.
Click the Links Below to Access the App
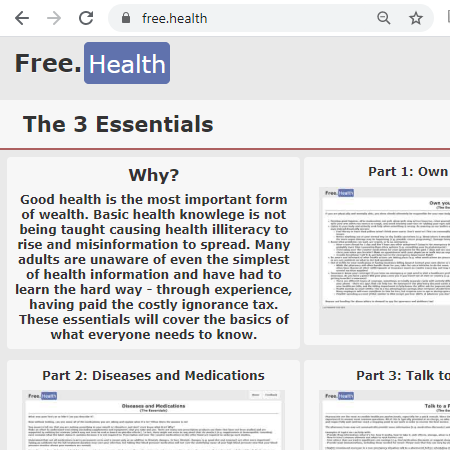
Free.Health
Covers the bare-minimum, essential health information needed to cover most of our health needs.
Click the Links Below to Access the App

Math is Hard
A math puzzle game where you attempt to reach an end value from a starting value and some operations.
Click the Links Below to Access the App